erf的近似实现

第二次读这本书了（第一次读是纸质版，第二次是微信读书上看的），当读到这一段时：

想到了“如何把Z Score转换为P值”这个疑问。于是，回顾了下：

对于正态分布$\mathcal{N}(\mu, \sigma)$，其概率密度函数为：

$$ PDF = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{z^2}{2}} $$

其累积分布函数为：

$$ CDF = \Phi(x) = P(Z \leq x) = \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{t^2}{2}}dt $$

考虑到误差函数(Error Function)

$$ erf(x) = \frac{2}{\sqrt{\pi}}\int_{0}^{x}e^{-t^2}dt $$

可以将累积分布函数采用erf来进行计算，即有：

$$ CDF = \frac{1}{2}\big[1+erf(\frac{x-\mu}{\sigma\sqrt{2}})\big] = \frac{1}{2}\big[1+erf(\frac{z}{\sqrt{2}})\big] $$

Excel或者是WPS下相关的公式是NORMDIST，在Python中可以用scipy.stats.norm.sf。

比如要计算书中例子，投资回报率15%，年误差率10%，那么任何一年赚钱的概率93%，可以这样计算：

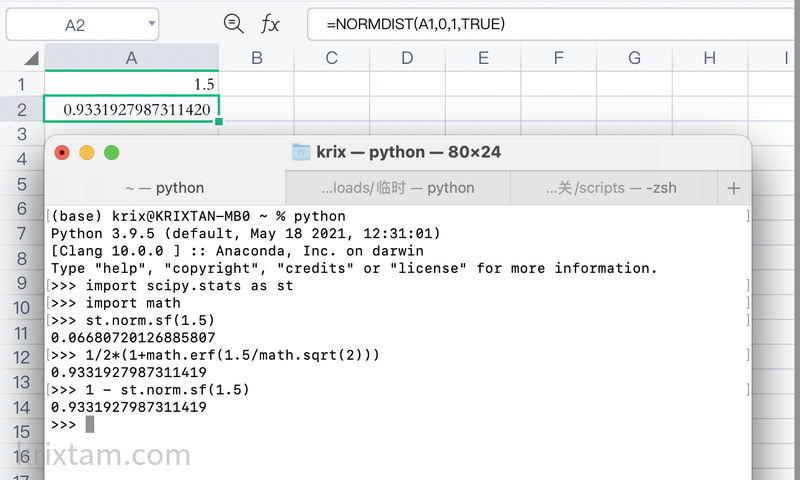
最后，因为好奇心下，又去找了下实现，比如：

C语言实现代码参考

发现了Netlib这个好地方，如果可以快速索引的话，可能里头很多方法的源码实现都可以好好研究下

MATLAB的erf是基于”Rational Chebyshev Approximations for Error Function –W.J.Cody”实现的，可以参考这里

实际上，用近似实现可以简化，误差方面，也还是可以接受，试了一下：

• Numerical approximations
  • $ erf(x) = sgn(x)(1 - t \cdot e^{-x^2 - 1.26551223 + 1.00002368t + 0.37409196t^2 + 0.09678418t^3 - 0.18628806t^4 + 0.27886807t^5 - 1.13520398t^6 + 1.48851587t^7 - 0.82215223t^8 + 0.17087277t^9}) $，其中$ t = \frac{1}{1 + \frac{1}{2}|x|} $：0.9331927980409355
  • $ erf(x) = sgn(x)\sqrt{1 - e^{-x^2\frac{\frac{4}{\pi} + ax^2}{1 + ax^2}}} $，其中$ a = \frac{8(\pi - 3)}{3\pi(4 - \pi)} \approx 0.140012 $：0.9333201060994942
• Gauss Error Function Implementation for Javascript
  • Abramowitz and Stegun：0.9331913256227881
• A Simple Closed-Form Approximation for the Cumulative Distribution Function of the Composite Error of Stochastic Frontier Models

  我在本地也存了一份

  • $ erf(x) = sng(x)(1 - e^{-1.09500814703333x - 0.75651138383854x^2}) $：0.9331733961643032

Python写了这4个算法的测试，可以从这里下载源文件