关于盈利概率的思考

昨天跟同事讨论“某基金持有1年的时间的盈利（不亏本）的概率是多少”这个问题。

我同事的算法是：

1. 假设统计的是某个时间段（比如近10年）情况，标记为统计时间区间
2. 假设投资者每天都申购一笔并持有1年后赎回并计算该笔交易的收益率，然后从统计时间区间内，计算得到的收益率序列
3. 将收益率序列中，收益率大于或等于零的样本数，除以，总样本数，获得该基金持有1年的时间的盈利（不亏本）的概率

我昨天建议改用正态分布的方式去做（前面两点假设一样）：

1. 假设统计的是某个时间段（比如近10年）情况，标记为统计时间区间
2. 假设投资者每天都申购一笔并持有1年后赎回并计算该笔交易的收益率，然后从统计时间区间内，计算得到的收益率序列
3. 通过收益率序列，基于正态分布的假设下，算出均值、方差从而计算出其盈利概率

昨天我认为我同事的算法不是在计算概率，而更多算的是一种频度；今天早上想起了泊松分布，在想是否可以用其他的分布来去解释这个所谓的“盈利概率”，最后得到了如下的答案：

• 我同事用的是伯努利分布（Bernoulli distribution），属于离散型概率分布
• 我用的是正态分布，属于连续概率分布

其实都没有错！

在回顾二项分布（Binomial distribution）、几何何分布（Geometric distribution）以及泊松分布（poisson distribution）的过程中，发现了韩国小伙伴分享的这个分布关系图不错；为了方便查阅，我本地放一份作为备份

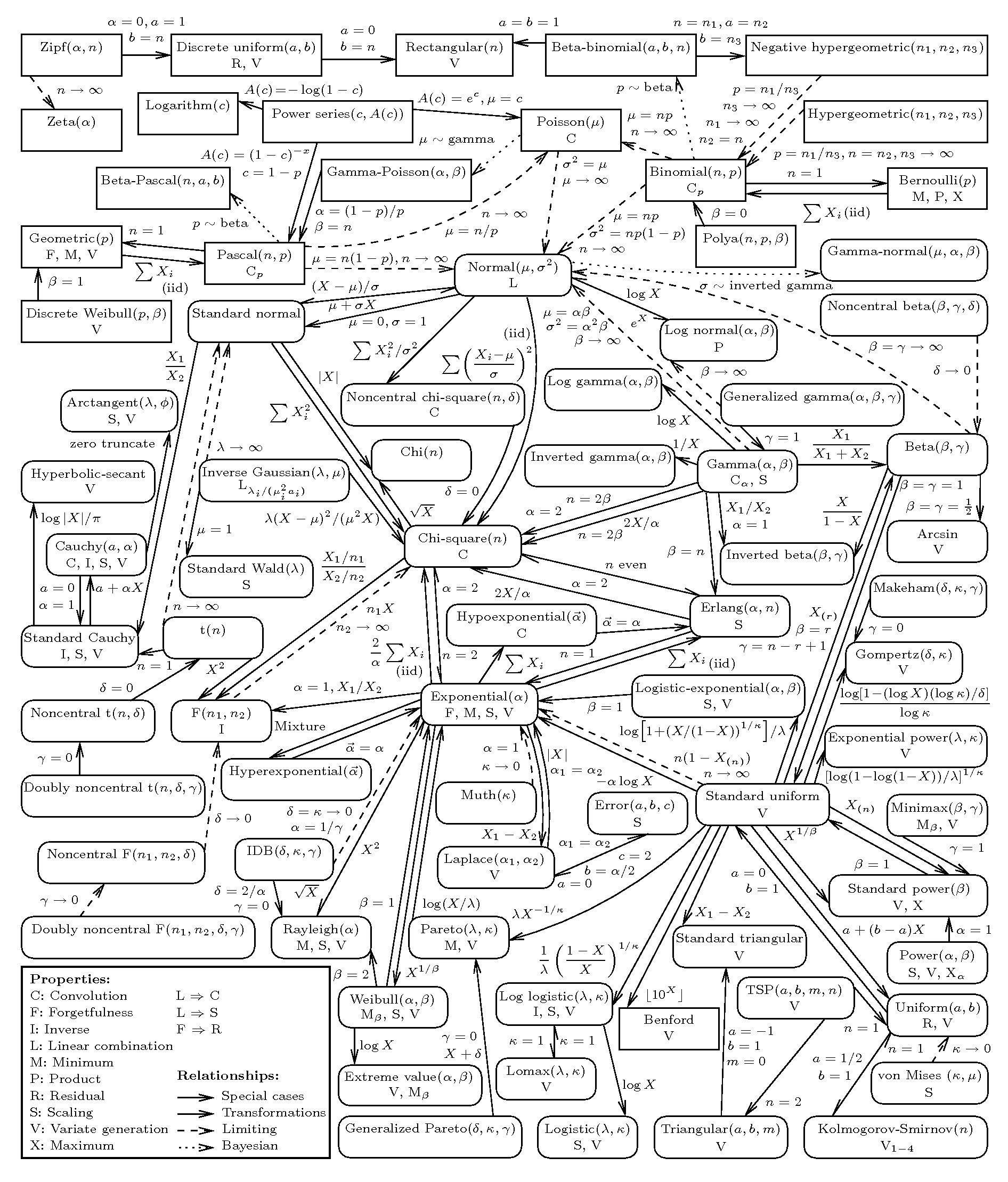
另外，通过查阅知乎上《二项分布、泊松分布和正态分布的区别及联系?》，还发现了一个有趣的数学统计知识归纳分享：语雀